{[userprofile.firstName]} {[userprofile.lastName]}
{[userprofile.totalFollowing]} Followers
{[userprofile.totalFollowed]}
{[userprofile.bio]}
{[userprofile.gender]}
{[userprofile.town]}
{[userprofile.state]}
{[userprofile.realNumber]}
{[userprofile.website]}
-
[ended]Mathematics Tutoring Session #12[Mapping and Function(Wed. 2rd march 2016, 4:00 - 5:00pm)]
Mathematics
Emmanuel Iwara(Tutor)
02-03-2016 13:04:00 +0000This session has ended for today
Good day all
The concept of Mapping and Function is the most fundamental in mathematics often tested on JAMB and other exams. so lets take a quick look into this topics.
Mapping - Given two non-empty set A and B, if there is a rule, which assigned an element x∈A a unique element y∈B,then such rule is called mapping.
The set A is called the Domain of the mapping, while the set B is called the co-domain of the mapping.
e.g see (Image (1) below) for Domain and Co-domain.
From (Image 1), the set { 2, 5, 4, 1} is the Domain, while the set {3, 6,10, 20} is the Co-domain.
3 is the image of 2, 20 is the image of 1, 10 the image of 4 and 6 the image of 5.
The collcetion of all the images is what is called the Range.
Example 1.Determine the domain of the mapping f: x → 2x-3.If C = {-3, -1, 5} is the range and f is defined on D.
Solution
2x -3 is the formula connecting the parent set (Domain) and the Co-domain (range)
Now by assumption what will be the value of (x) that when substitute into (2x-3) will give -3, -1, 5. then those numbers are elements of the domain.
Observe that when x = 0,f: x → 2x-3 = 2(0)-3 = -3, and when x = 1,f: x → 2x-3 = -1, and when x = 4, f: x → 2x-3 = 2(4)-3 = 5.
. Hence the domain of the mapping are {0, 1, 4} that gives the co-domain {-3,-1,5}.
One -One- Mapping,- let f: x →Y be the mapping that establishes that the correspondence between the sets X and Y.The mapping f is called a One to One if different elements in the domain X have different images in the co-domain Y.
e.g The mapping which associates each University in Nigeria with its Vice - Chancellor.
From (Image 1) (3 is the image of 2) and (6 is the image of 5)
Onto -Mapping -Let f: x →Y be mapping from the set X to the set Y.The mapping f is called Onto -mapping if every element of the co-domain is an image of atleast one element in the domain.
e.g (See Image 2 below), the range is equall to the co-domain.
Composite Mapping - Let f: x →Z and g: Z→Y be two mappings such that the co-domain of f is the domain of g.
The mapping gof is called composite mapping.
Example 2. Let the mapping f and g on the set of real numbers be defined by f(x) = x2 + 2 and g(x) = 2x + 1.
Find;
(i) gof
(ii) fog
Solution
i) gof = g[f(x)] = 2( x2 + 2) + 1.
That is putting the value of f(x) into (x) in g(x)
= (2x2 + 4) + 1.
= 2x2 + 5.
ii) fog = f[g(x)] = (2x + 1)2 + 2.
That is putting the value of g(x) into (x) in f(x),which give us.
= 42+ 4x + 1 + 2
= 42+ 4x + 3.
Example 3. If f and g are mappings defined over the set of real numbers by f(x) = (x+3) and g(x) = 2x2 + 3 respectively, find the value of x for which fog = gof
Solution
fog = f[g(x)] = (2x2 + 3 + 3)
That is putting the value of g(x) into (x) in f(x)
= 2x2 + 6
gof = g[f(x)] = 2(x+3)2 + 3.
That is putting the value of g(x) into (x) in f(x)
[2(x+3)(x+3)] + 3
= 2[x2 + 6x + 9] + 3
= 2x2 + 12x + 18 + 3
Then fog = gof will be
2x2 + 12x + 18 + 3 = 2x2 + 6
Collecting terms
12x + 21 = 6
12x = -15
x = -15/12.
Inverse Functions - A function f has an inverse, if it is both ono to one and onto.
ie the domain of f is the range of f1 and the domain of f1 is the range of f.
Example 4.The function f over the set of real numbers is defined by f(x) = (1/3)x + 2. Find f1.
Solution
Let y = (1/3)x + 2
y-2 = (1/3)x
x = 3(y-2)
∴ x = f′(y) = 3(y-2)
replacing y by x
f′(x) = 3(x-2)
Now see if you can try the following past Jamb and other exams questions.
1.The function f and g on the set of real numbers are defined by f(x) = 3x-1 and g(x) = 5x + 2 respectively.
Find;
(a) fog
(b) gof
2.If f and g are mappings defined over the set of real numbers by f(x) = (x-1) and g(x) = 2x2 - 2 respectively, find the value of x for which fog = gof
3.Given the functions.
f(x) = 3x2 - x + 5.
g(x) = 5x + 3.
Simplify f(x) + 3g(x).
4.If f(x) = (x-1)/(x2 -1), find f(1-x)
5.Determine the inverse function of f(x) = 2x +3.
Don't forget to fill our the survey after the session:
Survey Feedback Link - http://goo.gl/forms/Tasr40Ck1Z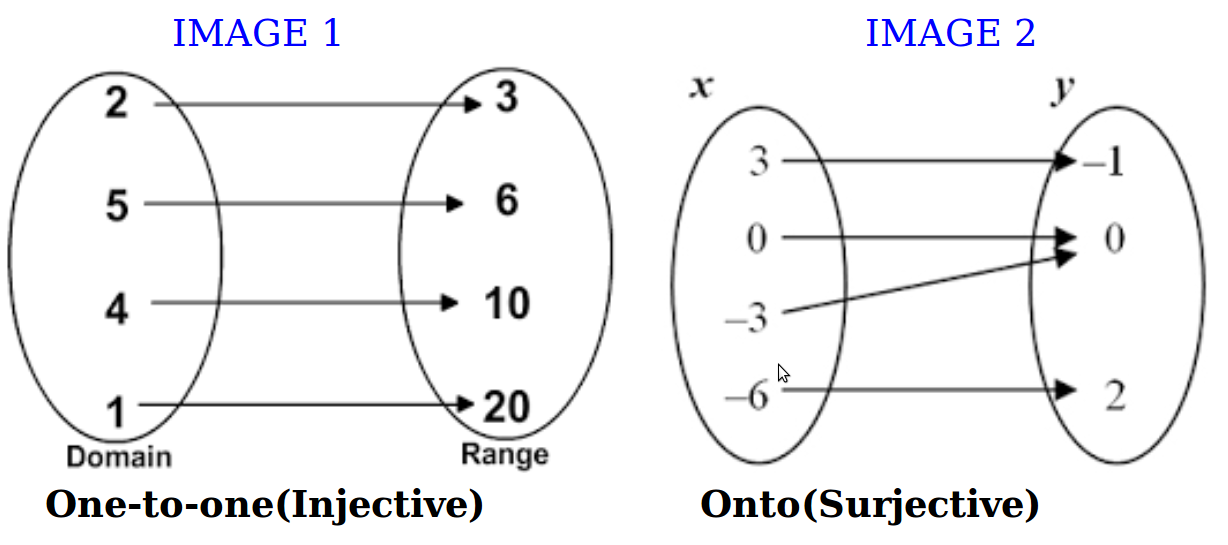
-
Emmanuel Iwara(Tutor)
Hello class am Emmanuel ready to answer all your problem if you have any on mapping and function feel free to ask.
0 02-03-2016 15:07:00 +0000
-
Joey Hogan
I think you should give a Brife summary on mapping, seeing that I just joined.
0 02-03-2016 15:19:00 +0000
-
Emmanuel Iwara(Tutor)
@Joey Hogan Given two non empty sets A and B, the rule which assigns an element a element A a unique element y element B is called Mapping.e.g 2 maps to 3, 5maps to 6 in the Image attach above.
0 02-03-2016 15:29:00 +0000
-
Emmanuel Iwara(Tutor)
@Joseph Utih please go through the script for more clearification
0 02-03-2016 15:31:00 +0000
-
{[reply.name]}
{[reply.voteCount]} {[reply.voteCount]} {[reply.created]}
{[reply.voteCount]} {[reply.created]}