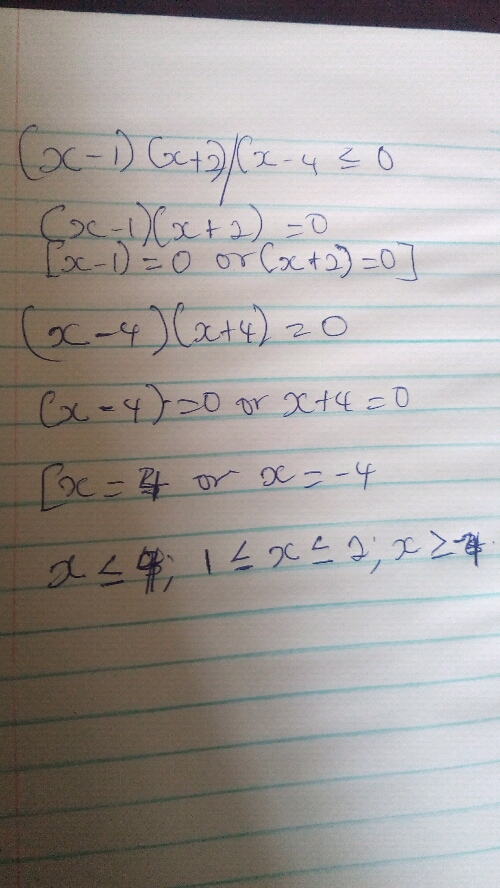{[userprofile.firstName]} {[userprofile.lastName]}
{[userprofile.totalFollowing]} Followers
{[userprofile.totalFollowed]}
{[userprofile.bio]}
{[userprofile.gender]}
{[userprofile.town]}
{[userprofile.state]}
{[userprofile.realNumber]}
{[userprofile.website]}
-
[ended]Mathematics Tutoring Session #11 (Linear Inequalities[Tues. 1st Mar 2016, 3:00 - 4:00pm])
Mathematics
Emmanuel Iwara(Tutor)
01-03-2016 12:40:00 +0000Linear Inequality is most fundamental in the world of mathematics often tested by Jamb and other exams.
This session has ended for today
In mathematics a linear inequality is an inequality which involves a linear function. A linear inequality contains one of the symbols of inequality: < is less than. > is greater than. ≤ less than or equal to.≥ greater than or equal to.
Solving inequalities does not create any problem, as the approach, manner and steps are the same as in linear equations.
Example 1 .Solve the inequality 4x + 12 <2
Solution
4x < 2 - 12(collecting like terms)
4x <-10
x < -10/4
x< -5/2
Example 2. Solve the Inequality
(3x + 4)/ x ≥ 3x/(x + 2)
Solution
Multiplying both sides by x(x+2)
x(x + 2)(3x + 4)/ x ≥ x(x+2)(3x)/ (x + 2)
= (x + 2)(3x + 4)≥ x(3x)
= [3x2 + 4x + 6x + 8) ≥ 3x2
Collecting like terms
3x2- 3x2 + 4x + 6x + 8 ≥ 0
= 10x + 8 ≥ 0
x = -8/10
Example 3. Solve the inequality
(2x2 + x ≥ x2 - 4x -6)
Solution
Collecting like terms we have
x2 + 5x + 6 ≥ 0
Factorizing
(x + 2)(x + 3) = 0
(x + 2 = 0 or x + 3 = 0)
(x = -2 or x = -3)
Example 4.Solve the inequality
6 < |x + 2|< 8
Solution
Case1
6 <|x+2|<8
x + 2 >6
x > 4
Case 2
(x + 2)< -6
x<-8
Thus
x>4 or x<-8
Also
|x + 2|<8
Case 1
x + 2 > 8
x > 6
and
Case 2
x + 2 > -8
x > -10
Written as -10<x < 6
Hence the solution to the problem above = (-10< x < -8 as well as 4 < x < 6)
Example 5. Example 5. Solve the rational inequality
(x2 - 3x + 2) / (x2 -9)≥ 0
Solution
(x2 - 3x + 2) / (x2 -9)≥ 0 = (x-1)(x-2)/(x-3)(x+3) when factorize
This rational function will be zero when the numerator is zero.
Thus
(x-1)(x-2) = 0
[(x-1) = 0 or (x-2) = 0]
[x = 1 or x = 2]
The rational function will be undefined wherever the denominator is zero.
Thus
(x -3)(x+3) = 0
(x-3) = 0 or (x+3) = 0
[x= 3 or x = -3]
Hence the solution is
x≤ -3; 1≤ x ≤ 2; x≥ 3.
Example 6.Solve |x-3| ≤6
Solution
Case 1.
x-3 ≤ 6
x≤ 6 +3
x≤ 9
and
x-3≥-6
x ≥-6 +3
x≥ -3
Hence solution is
x≥ -3 and x≤ 9
Now try and see if you can solve the following Past Jamb Questions
1. Determine the real numbers x satisfying x(x +x)>2.
2.List the Integers satisfying the inequality -2≤2x-6≥4
3. Find the range of values x which satisfy the inequality x/2 + x/3 + x/4 < 1
4.Solve the inequality (x-1)(x+2)/(x-4) ≤ 0
5.Solve |x+3| ≤ 4
-
Emmanuel Iwara(Tutor)
Hello class inequality is one of the most interesting topic one need to know as to advance in the world of mathematics. example 5 is less than x, implies that 5 is not inclusive but that the numbers are 1,2 3,and 4.
0 01-03-2016 14:15:00 +0000
-
Emmanuel Blessing
5. x is greater or equal to -1 and x is lesser or equal to 9
0 01-03-2016 14:16:00 +0000
-
Emmanuel Iwara(Tutor)
@Emmanuel Blessing x(x+2) is the L.C.M of the algebraic fraction (3x+4)/x greater than or equal to 3x/(x+2).
0 01-03-2016 14:21:00 +0000
-
Emmanuel Iwara(Tutor)
@Emmanuel Blessing thanks for giving a try ,but want you to check your working solution to no.4. Stay close the solutions to the questions will be post after the section is over.
0 01-03-2016 14:31:00 +0000
-
Emmanuel Iwara(Tutor)
@Omotayo thanks, but the question demand the real values of x
0 01-03-2016 14:33:00 +0000
-
{[reply.name]}
{[reply.voteCount]} {[reply.voteCount]} {[reply.created]}
{[reply.voteCount]} {[reply.created]}