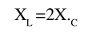{[userprofile.firstName]} {[userprofile.lastName]}
{[userprofile.totalFollowing]} Followers
{[userprofile.totalFollowed]}
{[userprofile.bio]}
{[userprofile.gender]}
{[userprofile.town]}
{[userprofile.state]}
{[userprofile.realNumber]}
{[userprofile.website]}
-
[ended]Mathematics Tutoring #9 Change of Subject Formula on Fri. Feb 2016 @ 4PM -5PM
Mathematics
Emmanuel Iwara(Tutor)
26-02-2016 13:19:00 +0000Good day all.
This session has ended for today
Change of subject formula is most fundamental in the world of mathematics often ask on Jamb and other exams.
Let quickly take a look at the following.
A FORMULA -Is a type of equation which shows the relationship blw different variables such as 'X' and 'Y'
Examples;
The subject of a formula - is the single variable to which everything else in the formula is equal. The subject of a formula will usually be positioned to the left of the equals sign.
For example:
x = 2y + 4z
Change of Subject Formula.
Whenever the subject of a formula is to be changed, the intention is to make the value becoming the subject stand alone and remain on the left hand side of the expression.
The methods used to effect this change may be any basic mathematical principles like multiplication, addition, subtraction, division, finding square roots, etc.
Whatever operation that is used to perform the change must be applied to both sides of the expression (formula).
1. Make u the subject of the formula;
v2 = u2 + 2as.
Solution
Step 1
Rearrange by bringing (u2) to the LHS of the expression and carrying (v2) to the RHS of the expression. The reason for this is because you have been instructed to make (u) the subject of the formula according to the question.
-u2 = 2as – v2.
Note; Whenever you carry figures from one side of an expression to another, the sign changes to the opposite.
Step 2
Multiply both sides by -1.
u2 = -2as + v2
Step 3
Take square root of both sides;
u = √(-2as + v2)
Example 2.
Make b subject of the equation.
a(b + c) + 3/d + 2 = 0
Solution.
Step 1.
Multiplying out the bracket will yield
ab + ac + 3/d + 2 = 0.
The intention is to make the value becoming the subject stand alone and remain on the left hand side of the expression.
ab = 2-3/d -ac
Considering the right- hand side of the equation and taking L.C. M, we have
ab = (2d -acd -3)/d Dividing through by a, gives
b = (2d -acd -3)/ad.
Example 3.
Make w the subject of the formula
S = √4/v − w/3---------------------(1) Solution
Squaring both sides of equation (1) will now give us S2 = 4/v − w/3
The intention is to make the value becoming the subject stand alone and remain on the left hand side of the expression.
w/3 = 4/v −S2 ------------------(2)
Taking L.C.M of the right -hand side of equ (2) becomes
w/3 = (4-s2v)/v
Cross - multiplying
w = 3(4-s2v)/v
w =( 12-3s2v)/v
Following the examples above.
Can anyone try solving the following past JAMB QUESTIONS.
1.Make c the subject of the equation.
a(b+c) + 5/d -2 = 0.Jamb Question Number (26), 1979.
2. Make v the subject of the formula.
S = √(4/v − w/3)
3.If gt2 - k -w = 0.
make g the subject formula.Jamb Question Number (3),(2015)
4.Make f the subject of the formula
T = cfd3/16
and find the value of f when T = 2 and d = 3.
Help us improve these tutoring sessions!
We would love to hear back from anyone that participated in this session:
Survey Feedback Link - http://goo.gl/forms/Tasr40Ck1Z
-
{[reply.name]}
{[reply.voteCount]} {[reply.voteCount]} {[reply.created]}
{[reply.voteCount]} {[reply.created]}