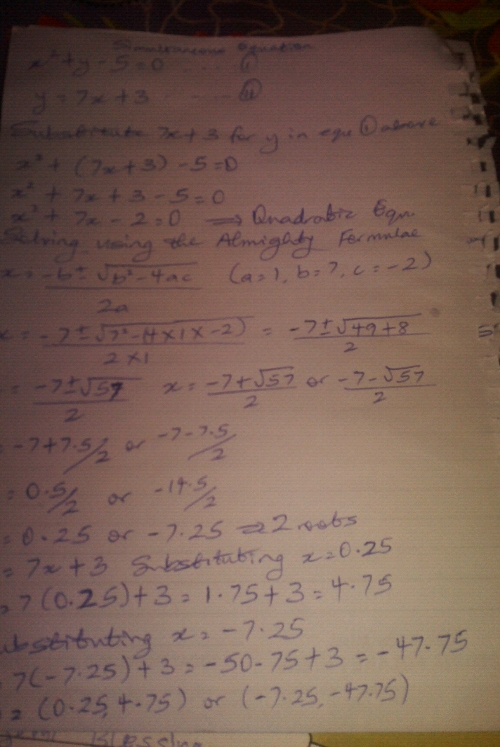{[userprofile.firstName]} {[userprofile.lastName]}
{[userprofile.totalFollowing]} Followers
{[userprofile.totalFollowed]}
{[userprofile.bio]}
{[userprofile.gender]}
{[userprofile.town]}
{[userprofile.state]}
{[userprofile.realNumber]}
{[userprofile.website]}
-
Selected Questions From Some Federal Universities Post UTME
Mathematics
Chima Sunday (Tutor)
15-06-2016 12:34:00 +0000Try and do justice on these questions, as rightly said that practice makes one better. Please Show working on paper and include a picture of your hand written Solution in your response. Wish you the best!
1. Solve the following simultaneous equations for x
x2 + y - 5 = 0
y = 7x + 3
A. 2,4
B. -2,4
C. -1,0
D. 1,-8Updated Solution
x2 + y - 5 = 0 ---------(1)
y = 7x + 3 -------------------(2)
putting (2) into (1)
x2 + 7x + 3 - 5 = 0
x2 + 7x - 2 = 0
using completing the sqaure
x2 + 7x = 2
x2 + 7x + (7/2)2 = 2 + 49/4
(x + 7/2)2 = (8 + 49)/4 = 57/2
x = 7/2 + √57/2 or 7/2 - √57/2
x = (7 + √57)/2 or (7 - √57)/2
so from the Optional given, it is wise to conclude that its option not there2. If y = 3x2 (x3 + 1)1/2, find dy/dx
A. [6x(x3 + 1) + 3x2]/2(x3 + 1)1/2
B. [12x(x3 + 1)3x2]/2(x3 + 1)1/2
C. [15x4 + 6x]/6x2(x3 + 1)1/2
D. [12x(x3 + 1) + 9x4]/2(x3 + 1)1/2Updated Solution
y = 3x2(x3 + 1)1/2
we use the product rule
dy/dx = vdu/dx + udv/dx
where u = 3x2, du/dx = 6x
v = (x3 + 1)1/2
we apply function of function to obtain
z = x3 + 1, dz/dx = 3x2
so v = z1/2, dv/dz = 1/2(z)1/2 = 1/2(x3 + 1)1/2
thus dv/dx = dv/dz * dz/dx = 3x2 * 1/2(x3 + 1)1/2 = 3x2/2(x3 + 1)
dy/dx = vdu/dx + udv/dx
= (x3 + 1)1/26x + 3x2*3x2/2(x3 + 1)1/2
so dy/dx = 6x(x3 + 1)1/2 + 9x4/2(x3 + 1)1/2
to simplify further by finding LCM
[12x(x3 + 1) + 9x4]/2(x3 + 1)1/2
So correct Option is D
-
Adeyemi Blessing
Above is my solution to No. 1 question. Although I didn't get any answer relating to the options given but it could be option A. Waiting for my correction & the right solution/explanation/answer.
1 15-06-2016 18:34:00 +0000
-
Adeyemi Blessing
Above is the check work of my answers 0.25,4.75 or -7.25,-47.75 which is the root of the equation for x & y respectively. For question no. 1
1 15-06-2016 18:53:00 +0000
-
Chima Sunday (Tutor)
thumb up to you Adeyemi Blessing for that wonderful and fearless bold attempt,. keep the fire burning the sky will be your run way. Please do note that the solution to the post has been updated, so try and check it up. Once again thank you.
1 17-06-2016 16:16:00 +0000
-
Kelechi Umejiaku
X²+y-5=0 Y=7x+3 Sol Putting eq(2) into eq(1) X²+7x+3-5=0 X²+7x-2=0 Its now a quadratic equation Using general formula -b±√b²-4ac/2a -7±√7²-4×1(-2) -7±√47+8 -7±√57 -7+√57/2=0.3 or 7+√57/2= 7.3
1 26-07-2016 00:07:00 +0000
-
{[reply.name]}
{[reply.voteCount]} {[reply.voteCount]} {[reply.created]}
{[reply.voteCount]} {[reply.created]}